Self Focusing and Defocusing
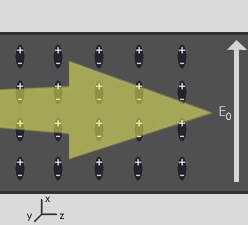
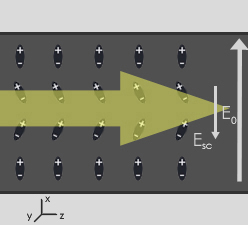


Among interesting phenomena observed in photorefractive (PR) materials are light beam self-focusing and self-defocusing and the formation of optical spatial solitons. The processes leading to these effects are illustrated in figure on the right. In the absence of applied electric field, polar chromophores (shown as dipoles) in a typical PR organic thin film are randomly oriented. As the electric field E0 is applied, the dipoles align. If the light beam is sent through the PR device in the direction perpendicular to applied electric field, the light generates charge carriers that drift in the electric field, get trapped and create a space-charge field Esc counteracting the applied field E0 in the illuminated part of the device. Then, the total electric field in the illuminated part is lower than that outside of the light beam, which leads to a partial relaxation of the chromophores in the illuminated portion of the device. Since in PR materials, refractive index is electric field-dependent, a non-uniform electric field distribution along x-axis leads to a non-uniform refractive index profile.
Depending on the polarization of the beam with respect to the direction of the applied electric field, this refractive index profile leads to either self-focusing or self-defocusing of the beam. The total refractive index change (Δn) in orientationally enhanced PR materials with birefringence component ΔnBR dominating over electro-optic component ΔnEO for x- and y-polarized light is:M. Shih and F. Sheu, Opt. Lett. 24, 1853 (1999), F. Sheu and M. Shih, J. Opt. Soc. Am. B 18, 785 (2001)
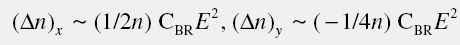
where n is the refractive index, E is the total electric field, and CBR is a constant defined here. Since the total electric field in the illuminated part of the sample is lower than that in the non-illuminated part, the x- (y-) polarized beam experiences lower (higher) refractive index compared to non-illuminated part, which leads to beam self-defocusing (self-focusing). At a certain magnitude of electric field E0, the self-focusing effect exactly compensates for the diffraction, and an optical spatial soliton, i.e. the beam that preserves its spatial characteristics as it propagates through the film, forms. In this case, the beam shape at the output plane of the sample is identical to that at the input plane. This self-trapping effect is useful whenever beam propagation in a material over some distance is required.Z. G. Chen et al., Opt. Lett. 28, 2509 (2003), M. Asaro et al., Opt. Lett. 30, 519 (2005)